
三次元測定機で測定する幾何公差で振れ(全振れ含む)は、
同じワークを再測定しても全然違う数値が出てしまう事ありませんか?
特に基準円筒が短いワークに現れる現象です。
少し説明したいと思います。
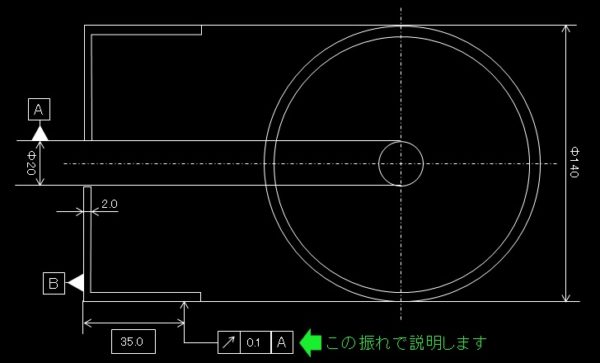
簡単な製品図を描いてみました。
基準径Φ20の板厚2.0mm、外径Φ140のカップ状の製品です。
振れの指示部位は外径Φ140の高さ35mm部とします。
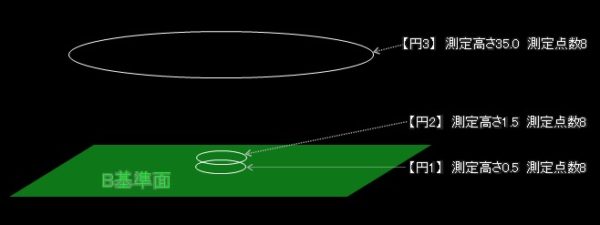
板厚2.0なので基準径は高さ0.5と1.5部を円測定します。
振れが指示されているΦ140外径は指示通り高さ35を測定します。
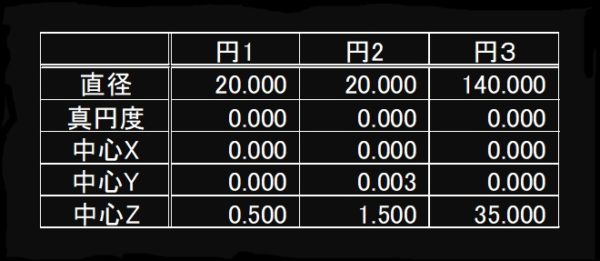
円を測定した結果は以下の通りとしました。
実物では有り得ないですが真円度0.000の完全円としてます。
この結果で円筒A基準の振れを算出すると0.207となり規格外となります。
表を見てお判りの通り、原因は円2の円中心Y:0.003です。
たかが3ミクロンの中心ズレがこんなに効くのか…?! と思われたのではないでしょうか?
すこし分かり易くグラフにしてみます。
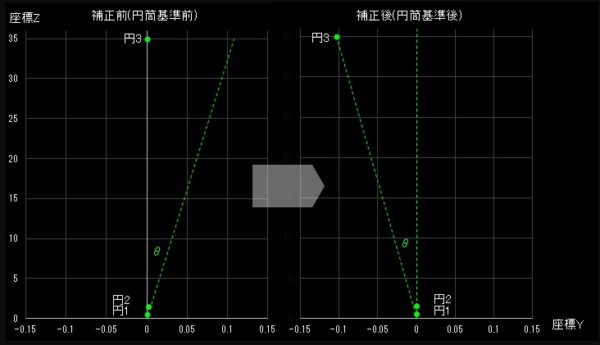
それぞれの円のY座標とZ座標をグラフに表現しました。
円1と円2は基準円筒の為、円2の円中心Y:0.003をY:0.000となる様に補正します。
補正した分(Θ)だけ円3の中心座標が移動します。
円3の円中心はX:0.000 Y:-0.103と言うことになります。
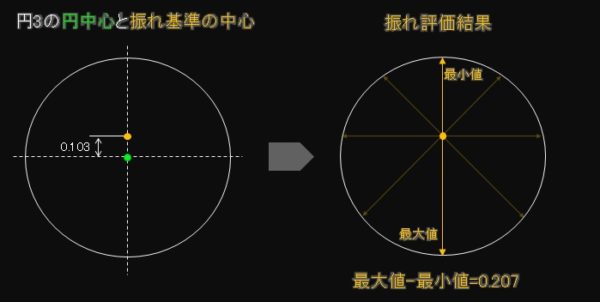
最後に演算実測値を簡単に図解にしてみました。
0.003レベルの円中心座標差が規格値に大きく影響する事がお判り頂けたのでないでしょうか?
『三次元測定機の数値を信頼していない』と言う声を耳にしますが、
一概にそうとも言えない事に納得頂ける内容かと思います。
今回の様な数値が安定しない『振れ』の解決案としては設計変更が妥当なケースだと判断します。
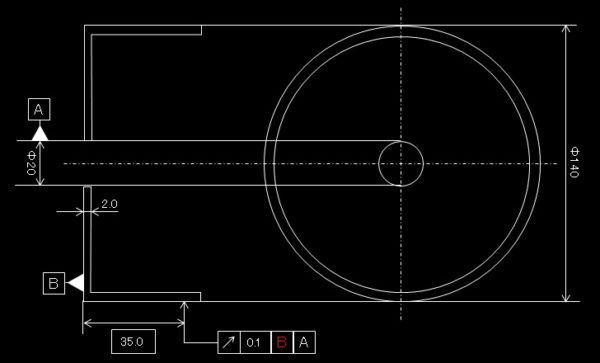
どうでしょうか?最初の図面と比較してみて下さい。
第一基準にB基準を追加しただけですが、A基準円筒の微々たる影響を受けずに測定結果が安定します。
(マンドレルで測定するにしても測定し易さば格段にアップですよね!)
弊社に測定業務を依頼して頂ければ、
本件の様な説明と今後の解決案含めて提案させて頂きたく考えております。
是非ご相談ください。宜しくお願いします。

