
製造業に従事されている方であれば、
真円度の算出方法は『最大半径と最小半径の差=真円度』は認識されている事と思います。
今回、円中心を気にする方ってあまり居ないのでは…と思いブログをUPさせて頂きました。
円中心をの算出する円の算出方法は4種類ありますので、
この算出方法によって円中心の位置が変わる事例を紹介したいと思います。
さすがに計算式を説明出来るまで理解できていないので、
変な突っ込み無しで読んで頂ければと思います。
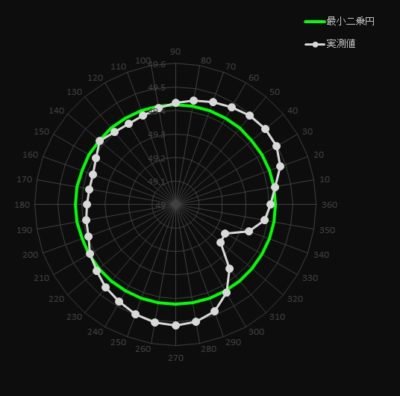
1、最小二乗法
偏差の最小二乗和が最小となる円が緑の円となります。
計算は全部の測定点を使って計算しています。
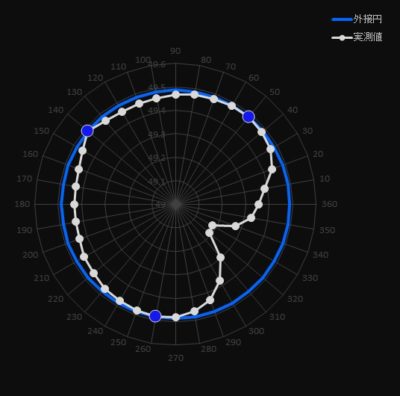
2、外接法
測定点の最も外側の3点で作られる円が青の円となります。
この波形ですと青〇の点を通る円となります。
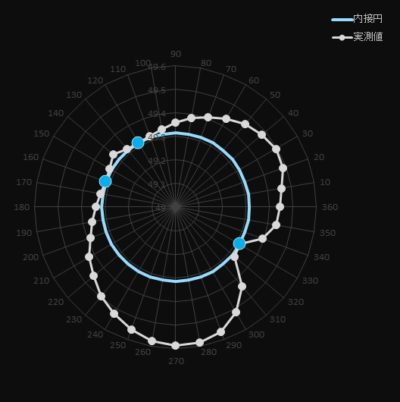
3、内接法
測定点の最も内側の3点で作られる円となります。
点の抽出方法は外接法と相反する考え方です。
外接法と内接法はかなり理解し易いと思います。
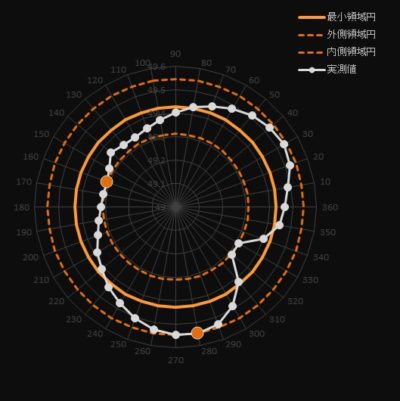
4、最小領域法
全ての測定点が入る様に外側と内側の円を描き(破線の2円です。)
2円の差が最も小さくなる円となります。(実線の円です。)
ちなみに破線の円は内接&外接円とは違います。
では、この算出方法の違う円中心がどの程度違うのか散布図に表現してみました。
どうです?結構違いませんか?!
個人的には最小二乗法と最小領域法の円中心がこんなにも違うモノだと思いませんでした。
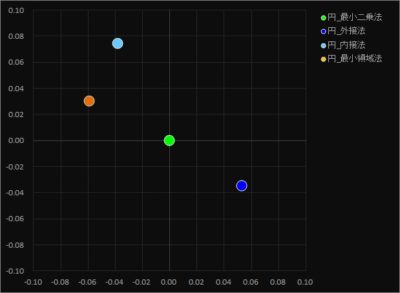
この4つの円中心から分かり易く真円度を横並びにしてみると以下の様な結果になりました。
今回のサンプルデータは分かり易く表現する為に、かなり円形状が悪いデータを使用しましたが…
結構、数値に差が出ましたね…。
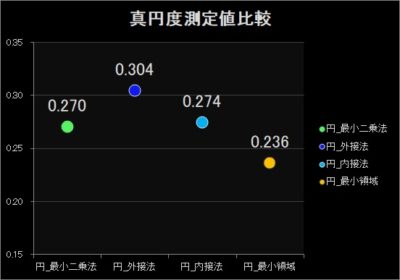
もし仮に規格が0.25以下だった場合… と思うと、恐ろしいですね。
3次元測定機のプログラム作成時、円測定する際にどの評価方法を使用しているのか今一度確認しましょう!
そもそも、この手のミスは気づいていない場合が多いので、是非一度見直してみることをお勧めします。

